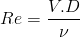ATTENTION : LA SÉCURITÉ EST L'AFFAIRE DE SPÉCIALISTES, MÊME POUR LES PETITS BARRAGES. CE SITE NE PEUT SE SUBSTITUER A DES BUREAUX D'ÉTUDES SPÉCIALISÉS
Calcul des écoulements en charge
L'hydraulique repose sur deux principes fondamentaux :
- l'eau coule toujours naturellement du point haut vers le point bas
- l'eau se fatigue en s'écoulant
Ces principes fondamentaux nous permettront de calculer la vitesse et
donc le débit de l'eau dans des conduites en charge. Que
signifie en charge ? Ca veut simplement dire que l'ensemble de la
section d'un tuyau est remplie d'eau, ce qui se traduit par la
présence d'une pression variable dans le système.
Cette dernière est comprise entre la pression de
vaporisation de l'eau (- 10 mètres de colonne d'eau dans le
cas d'une forte aspiration) et la pression de rupture de
l'installation. Les écoulements en charge se
différencient donc des écoulements à
surface libre pour lesquels la pression de la veine fluide la plus
haute est égale à la pression
atmosphérique.
Charge et pertes de charge
Un écoulement en charge se définie
premièrement par la hauteur entre le niveau haut et le
niveau bas, que l'on appelle la charge hydraulique (mesurée
en mètre de colonne d'eau mCE en hydraulique). Cette charge
est l'élément moteur des écoulements.
Mais comme l'eau se fatigue en s'écoulant il faut
également faire intervenir un terme de perte de charge qui
correspond à la dissipation d'énergie dans le
système. Pour simplifier les notations on mesure
également les pertes de charges en mCE. Vous avez donc
compris le principe de calcul en régime permanent :
satisfaire la relation charge motrice = pertes de charges.
Les pertes de charge se décomposent en deux familles. Les
pertes linéaire qui correspondent à la
dissipation d'énergie dans les tuyaux, et les pertes
singulières qui correspondent aux anomalies locales (coudes,
rétrécissement, sortie...). Les pertes de charges
linéaires se caractérisent par la
rugosité relative qui mesure le rapport entre la hauteur
moyenne des aspérités de la conduite
rapportées à la taille de la conduite (cf tableau
ci-après). Les pertes de charges singulières se
caractérisent elles par un coefficient k qui
dépend de la configuration du système (cf
également tableau ci-après)
Coolebrooke et Darcy
A partir de la formule de DARCY, les pertes de charge peuvent être
évaluées par
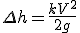
pour
les pertes singulières et par

pour les pertes de charge linéiques. La formule de
COOLEBROOKE permet d'estimer pour les pertes de charges linéaires
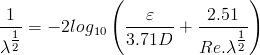
à partir notamment du
nombre de Reynolds qui vaut
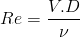
La
résolution de ces équation nécessite donc deux schéma numériques, l'un
pour calculer lambda en fonction de la vitesse, et l'autre pour faire
converger la vitesse vers la valeur qui permet d'égaliser les pertes de
charge et la charge disponible. MicroBarrage utilise la méthode de
NEWTON-RAPHSON et d'incrémentation contrôlée (oscillation du schéma de
NEWTON-RAPHSON).
Précision
La principale difficultée de
cette méthode de calcul réside dans le calcul du coefficient lambda. De
nombreuses méthode simplifiée ont été développées avant l'arrivée de
l'informatique. Les résultats sont très précis, mais dépendent toujours
des coefficients mis en entrée!
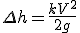 pour
les pertes singulières et par
pour
les pertes singulières et par  pour les pertes de charge linéiques. La formule de
COOLEBROOKE permet d'estimer pour les pertes de charges linéaires
pour les pertes de charge linéiques. La formule de
COOLEBROOKE permet d'estimer pour les pertes de charges linéaires 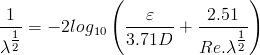 à partir notamment du
nombre de Reynolds qui vaut
à partir notamment du
nombre de Reynolds qui vaut